Filter Basics: Anti-Aliasing

This application note discusses the different filtering requirements for a sampled data system. It describes aliasing and the types of filters that can be used for anti-aliasing.

Filtering is such a common process that we often take it for granted. When we make a cell phone call, the receiver filters out all other channels so we only receive our unique channel. When we adjust the equalizer on a stereo system, we are selectively increasing or decreasing the audio signal in a particular frequency band, using a bandpass filter.

Filters play a key role in virtually all sampled data systems. Most A/D converters (ADCs) are preceded by a filter which removes frequency components that are beyond the ADC's range. Some ADCs have filtering inherent in their topology.

Let's take a look at a sampled data system, the filtering requirements, and the relationship to aliasing.

Background
The maximum frequency component a sampled data system can accurately handle is its Nyquist limit. The sample rate must be greater than or equal to two times the highest frequency component in the input signal. When this rule is violated, unwanted or undesirable signals appear in the frequency band of interest. This is called "aliasing."

For example, to digitize a 1kHz signal, a minimum sampling frequency of 2kHz is required. In actual practice, sampling is usually higher to provide some margin and make the filtering requirements less critical.

To help understand a sampled data system and aliasing, we look at a classic cinematography example.

In old western movies, as a wagon accelerates, the wheel picks up speed as expected, and then the wheel seems to slow, then stop. As the wagon further accelerates, the wheel appears to turn backwards! In reality, we know the wheel hasn't reversed because the rest of the movie action is still taking place. What causes this phenomenon? The answer is that the frame rate is not high enough to accurately capture the spinning of the wheel.

To help understand this, suppose a visible mark is placed on a wagon wheel and the wheel is spun. We then take snapshots in time (or samples). Since a movie camera captures motion by taking a certain number of snapshots per second, it is inherently a sampled data system. Just as the film takes discrete images of the wheel, an ADC takes a sequence of snapshots of a moving electrical signal.

When the wagon is first accelerating, the sample rate (the frame rate of the movie camera) is much higher than the revolution rate of the wheel, so the Nyquist criterion is met. The camera's sample rate is greater than twice the rate of revolution of the wheel, so it can accurately portray the wheel's motion and we see the wheel accelerating as expected (Figures 1a and 1b).

At the Nyquist limit, we see two points that are 180 degrees apart (Figure 1c). These two points typically are indistinguishable from each other in time by the human eye. They appear simultaneous and the wheel appears to stop. At this wheel speed, the rate of the rotation is known (based on the sample rate), but the direction of the spin cannot be ascertained. As the wagon continues to accelerate, the Nyquist criterion is no longer met, and there are two possible ways to view the wheel. We can "see" it as spinning forward and the other spinning in the reverse direction (Figure 1d).

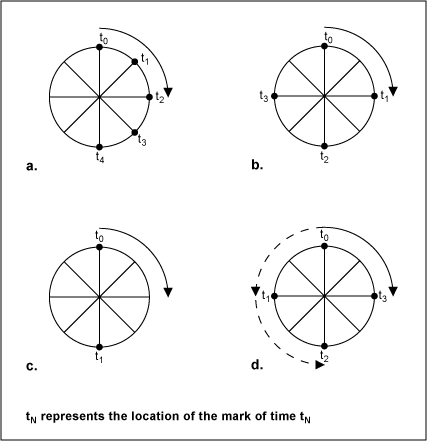
Figure 1. Wagon wheel example

Both can be viewed as the correct direction, depending on how you 'see' the wheel, but we now have an aliased signal. That is, there is a frequency component in our system that is unwanted and we cannot distinguish it from the real value. Both the forward and backward motion information are present. We typically see the backward component or "sub-multiple" or "image" of the forward component , because the primary forward component becomes unnoticeable due to the manner in which the eye/brain combination processes the data. Another interesting observation is that at the point where the sample rate is exactly equal to the rate of revolution of the wheel, the data obtained gives little useful information because the mark will always appear at the exact same point on the wheel. In this case one cannot tell whether the wheel is spinning or stationary.

Now moving into the mathematical realm, assume the wheel is a unit circle with sine and cosine coordinates. If one samples at the positive and negative peaks of the cosine values (which are 180 degrees out of phase), then the Nyquist criteria is met and the original cosine values can be reconstructed from the two sampled data points. Thus the Nyquist limit is essential in reconstructing the original signal. As more and more points are added, the ability to replicate the original signal improves.

Moving to the frequency domain, Figure 2 shows the frequency response of a sampled data system. Note the data is replicated at multiples of the sample rate (these are 'images' of the original signal); this is a fundamental characteristic of sampled data systems. In Figure 2a, the Nyquist criterion is met and there is no aliasing in the frequency band of interest. However, in Figure 2b, note how the Nyquist criterion is not met as the highest frequency in the band of interest is greater than half the sampling rate. The region of overlap is where aliasing occurs; a signal at frequency f_T also appears at f_T', similar to the aliasing example using the wagon wheel.

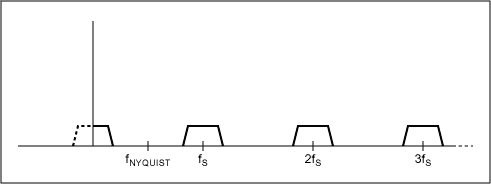
Figure 2a. Sampled data system frequency response with no aliasing.

Figure 2b. Sampled data system frequency response with aliasing.

Undersampling

Undersampling is a powerful tool that can be used effectively in selected applications. It allows an ADC to behave like a mixer in that it can take a modulated high-frequency carrier signal and create an image that is lower in frequency . In this way it behaves like a downconverter. Another key advantage is that it allows you to use an ADC with a sample rate that is lower than Nyquist, which usually has significant cost advantages. For example, assume we have a 10MHz modulated carrier with a 100kHz bandwidth (±50kHz centered at 10MHz). Undersampling at 4MHz yields first order sum and difference terms (f1+f2 and f1-f2) of 14MHz and 6Mz, and second order terms (2f1, 2f2, 2f1+f2, f1+2f2, | 2f1-f2 |, | f1-2f2) | of 8MHz, 20MHz, 18MHz, 2MHz, 24MHz and 16MHz. The image signal that appears at 2MHz is the one of interest. Note that we have taken a signal at 10MHz and by digitizing it have created an alias at 2MHz. We can now perform signal processing in the digital domain (filtering and mixing) to recover the original 50kHz signal. This approach removes the need for extensive analog processing, which is one of its key advantages. Since everything is done in the digital domain, to make changes in the performance and characteristics of the circuit, only the software needs to be modified. In contrast, for an analog design, the circuit hardware components and layout may need to change to modify the circuit's performance, and this can be quite costly.

One drawback of undersampling is that unwanted signals can appear in the desired band of interest and you cannot differentiate them from the desired signal. Also, when undersampling, the frequency range at the ADC input is often very wide. In the example above, even though our sample rate was 4MHz, the ADC front-end still has be able to acquire a 10MHz signal. In contrast, if an analog mixer is used in front of the ADC to shift the modulated carrier signal down to baseband, then the input bandwidth of the ADC would only need to be 50kHz rather than 4MHz, relaxing the ADC front-end and input filtering requirements.

Figure 3a. Undersampling example.

Figure 3b. Undersampling digitized image signals (1st and 2nd order).

Oversampling

Oversampling provides what is called a processing gain. When you over-sample, you are taking many more samples at a higher sampling frequency than needed and then filtering the data, thereby effectively reducing the noise floor of the system (we assume our noise is broadband white noise). This is different than averaging, where many samples are taken and the noise is averaged. Oversampling can be thought of in this manner: if the input signal is derived from a signal source that sweeps the input frequency, the frequency spectrum can be divided into ranges or "bins", each bin having a fixed width. The broadband noise is spread out over the entire frequency range of interest, so each bin has a certain amount of noise. Now if the sampling rate is increased, the number of frequency bins also increases. In this case, the same amount of noise is still present, but we have more bins over which to spread it. We then use a filter to remove the noise outside the frequency band of interest. The result is that each bin has less noise, and thus we have effectively reduced the noise floor of the system by oversampling.

As an example, if we have a 2ksps ADC (we use the Nyquist limit of 1kHz in the following formula) and a signal that is 1kHz, with a 1kHz digital filter following the ADC, the processing is given by: -10 log (1kHz/1kHz) = 0dB. If we increase the sample rate to 10ksps, the processing gain is now -10 log (1kHz/5kHz) = 7dB, or about 1-bit of resolution (1-bit is approximately equal to a 6dB improvement in SNR). By oversampling, the noise is not reduced, rather the noise has been spread out over a wider bandwidth, placing some of the noise outside the band of interest (with our digital filter) and thereby giving the effect that the noise has been reduced. This noise improvement is based on the following equation:

SNR improvement (dB) = 10 LOGA/B, where A equals the noise and B equals the oversampled noise.

Another way to state this is that oversampling reduces the in-band rms quantization noise by the square root of the oversampling ratio. Or, if the noise is reduced by a factor of two, there is an effective processing gain of 3dB. Keep in mind that we are only talking about broadband noise here. Other sources of noise and other errors cannot simply be removed by oversampling.

Anti-Alias Filters

With this background, we now move to anti-aliasing filters. When selecting a filter, the goal is to provide a cutoff frequency that removes unwanted signals from the ADC input or at least attenuates them to the point that they will not adversely affect the circuit. An anti-aliasing filter is a low-pass filter that accomplishes this. How does one select the right filter? The key parameters that need observation are the amount of attenuation (or ripple) in the passband, the desired filter rolloff in the stopband, the steepness in the transition region and the phase relationship of the different frequencies as they pass through the filter (Figure 4a).

Figure 4a. Actual filter.

An ideal filter has a "brick wall" response (Figure 4b). That is, it has an infinite transition ratio. However, this is never the case in real word applications. The steeper the rolloff, the higher the 'Q' or quality factor of the filter. And the higher the Q, the more complex the filters design. High Q's can lead to filter instability and self-oscillation at the desired corner frequency. The key to selecting the filter is to know the frequencies and the corresponding amplitudes of the interfering signals. For example, in cell phones, the designer knows the worst case amplitude and location of an adjacent signal and thus designs accordingly. Not all signals can be predicted in the frequency domain, and even some of the known interference signals are too large to adequately attenuate. But, based on the environment and application, you can account for known disturbances and design to minimize the effects of random interference to ensure more robust operation.

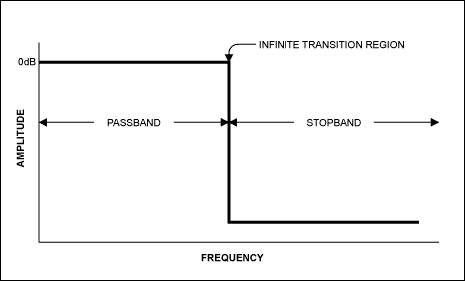
Figure 4b. Ideal filter.

Once the signal frequencies of interest are known, use a simple filter program to determine the filter topology needed to meet the passband, stopband, and transition region requirements. Of the four basic filter types, each has its own advantages (Figure 5).

Figure 5. Four basic filter types.

For example, the Butterworth filter has the flattest passband region, meaning it has the least attenuation over the desired frequency range. The Bessel filter has a more gradual roll-off but its key advantage is that it has a linear phase response, meaning each frequency component is delayed by an equal amount of time as it passes through the filter. A linear phase response is often specified as a constant group delay, since group delay is defined as the derivative of the phase response with respect to frequency. The Chebyshev filter has a steeper rolloff but more ripple in the passband. The Elliptic filter has the steepest rolloff. For a simple anti-aliasing filter, often times a simple single-pole passive RC filter is acceptable. In other cases an active filter (i.e., using an op amp) works well. One advantage of an active filter is that for multi-order filters, the operation of the filter is less sensitive to the values of the external components, in particular, the 'Q' value of the filter.

Anti-aliasing filters typically do not have to be exact with respect to the location of corner frequency so there is some leeway in the design. If, for example, you need maximal flatness, but there is still too much attenuation in the passband, simply moving the corner frequency out further could solve the problem. If the stopband attenuation is too low, increase the number of poles in the filter. Another solution is to amplify the signal after filtering it to increase the magnitude of the signal compared to the magnitude of the undesired signals.

Maxim provides the MAX274Filt, a software program that calculates the filter pole(s), zero(s) and 'Q' values, based on the filter requirements. The software also calculates the theoretical amplitude and phase plots for the filter. The software is actually a two-part program: the first half determines the poles and zeros, and the 2nd half is specifically for implementing these poles and zeros in the MAX274/MAX275 by calculating the resistor values needed to achieve the required filter response.

Maxim has a wide selection of low-power, lowpass filters that are ideal for anti-aliasing. These include the MAX7490 universal switched-capacitor filter, the MAX740x/MAX741x family of lowpass very small, low-power switched-capacitor filters, and the MAX274/5 universal continuous-time filters. Maxim also provides an abundant offering of low-power precision op amps for those wishing to design the filter themselves. For these users, a good filter handbook is a highly recommended reference book in the design process.

Reference

Delta-Sigma Data Converters Theory, Design, and Simulation, Edited by Norsworthy, Schreier and Temes, IEEE Press, ISBN 0-7803-1045-4.

January 2002

• Maxim/Dallas Glossary definition of aliasing
• Maxim/Dallas Glossary definition of anti-aliasing
• Maxim/Dallas Glossary definition of Nyquist
• Application Note/Tutorial: The Basics of Anti-Aliasing: Using Switched-Capacitor Filters

More Information		APP 928: Jan 11, 2002
MAX274: QuickView -- Full Data Sheet (PDF, 1.5M) -- Free Samples MAX275: QuickView -- Full Data Sheet (PDF, 1.5M) -- Free Samples MAX7400: QuickView -- Full Data Sheet (PDF, 200k) -- Free Samples MAX7401: QuickView -- Full Data Sheet (PDF, 208k) -- Free Samples MAX7403: QuickView -- Full Data Sheet (PDF, 200k) -- Free Samples MAX7404: QuickView -- Full Data Sheet (PDF, 200k) -- Free Samples MAX7405: QuickView -- Full Data Sheet (PDF, 208k) -- Free Samples MAX7407: QuickView -- Full Data Sheet (PDF, 200k) -- Free Samples MAX7408: QuickView -- Full Data Sheet (PDF, 152k) -- Free Samples MAX7410: QuickView -- Full Data Sheet (PDF, 144k) -- Free Samples MAX7411: QuickView -- Full Data Sheet (PDF, 152k) -- Free Samples MAX7412: QuickView -- Full Data Sheet (PDF, 152k) -- Free Samples MAX7413: QuickView -- Full Data Sheet (PDF, 144k) -- Free Samples MAX7414: QuickView -- Full Data Sheet (PDF, 144k) -- Free Samples MAX7415: QuickView -- Full Data Sheet (PDF, 152k) -- Free Samples MAX7418: QuickView -- Full Data Sheet (PDF, 412k) -- Free Samples MAX7419: QuickView -- Full Data Sheet (PDF, 412k) -- Free Samples MAX7490: QuickView -- Full Data Sheet (PDF, 232k) -- Free Samples MAX7491: QuickView -- Full Data Sheet (PDF, 232k) -- Free Samples
Download, PDF Format (73K)  AN928, AN 928, APP928, Appnote928, Appnote 928